Understanding the Mathematical Foundations Behind Large Language Models and Generative AI
Generative AI, particularly Large Language Models (LLMs) like ChatGPT, Gemini, or Claude, has taken the world by storm. From writing essays to generating code, these models can seemingly do it all. But behind the scenes, they rely heavily on mathematics. If you’re curious about what kind of math powers these systems — whether you’re a developer, student, or enthusiast — this blog will walk you through the essentials.
Why Mathematics Matters in Gen AI
Generative AI models don’t understand language the way humans do. Instead, they process numerical patterns through massive networks of computations. Math is the language that allows these models to learn, reason, and generate content.
Let’s break down the key areas of math that play a role in LLMs and Gen AI:
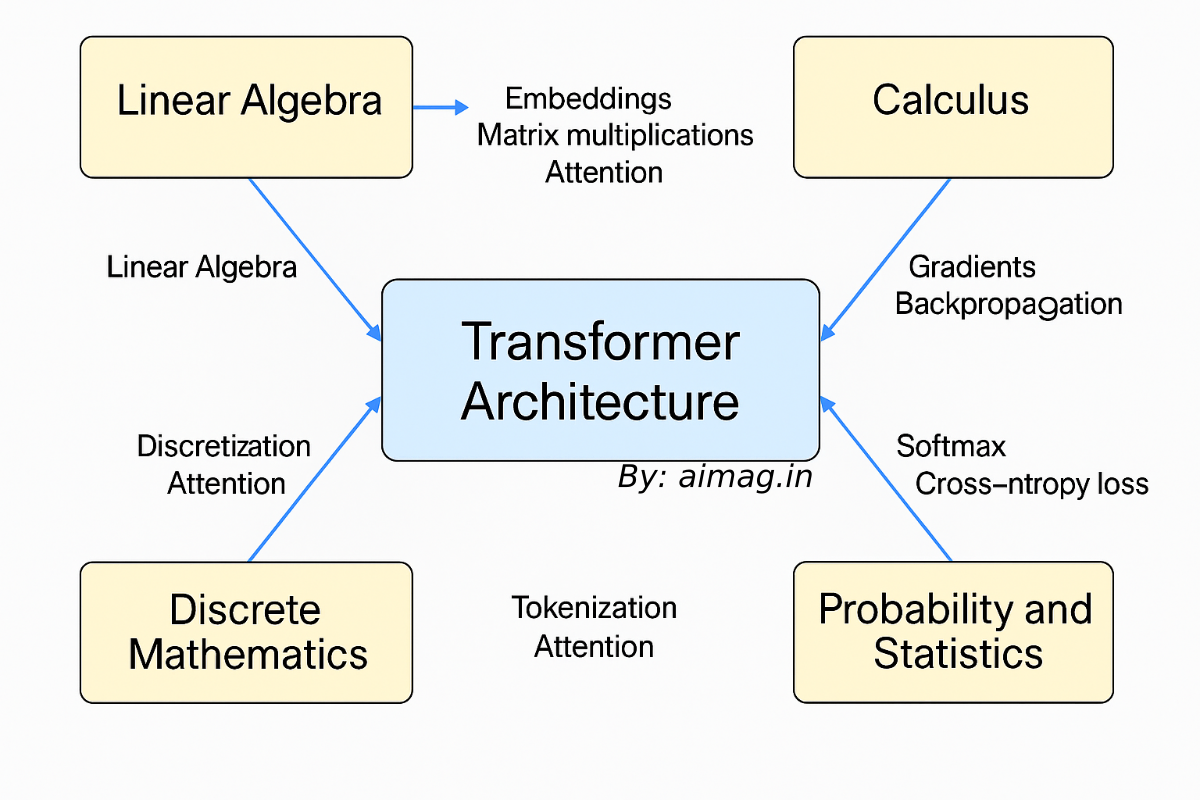
1. Linear Algebra – The Backbone of Neural Networks
LLMs are powered by neural networks, which depend heavily on linear algebra. Here’s how:
- Vectors and Matrices: Words and sentences are represented as high-dimensional vectors (embeddings). These are manipulated through matrix multiplications in each neural network layer.
- Transformers: The attention mechanism, which is central to LLMs, computes weighted averages of word vectors — a purely linear algebraic operation.
- Tensor Operations: Advanced generalizations of matrices (tensors) are used for computations across multiple dimensions.
Key Concepts to Know:
- Dot product
- Matrix multiplication
- Eigenvalues and eigenvectors
- Norms and orthogonality
2. Probability and Statistics – Modeling Uncertainty
LLMs are probabilistic at their core. Every word they generate is based on the likelihood of that word following a given sequence.
- Probability Distributions: LLMs use distributions like softmax to choose likely outputs.
- Bayesian Thinking: Some generative models incorporate ideas from Bayesian inference for updating beliefs as data is observed.
- Entropy & Information Theory: These help quantify the “surprise” of a word choice and are central to model training and evaluation (like cross-entropy loss).
Key Concepts to Know:
- Conditional probability
- Bayes’ theorem
- Entropy, KL divergence
- Random variables and expectation
3. Calculus – Training the Models
Training an LLM involves minimizing a loss function — a process rooted in calculus.
- Gradients: The gradient of the loss function with respect to model parameters is calculated using backpropagation.
- Partial Derivatives: Essential for understanding how changes in one parameter affect the overall function.
- Optimization: Techniques like gradient descent rely on derivatives to adjust weights during training.
Key Concepts to Know:
- Derivatives and gradients
- Chain rule
- Gradient descent
- Jacobian and Hessian matrices
4. Discrete Mathematics – Structure and Logic
Natural language is discrete, and understanding its structure involves logic and combinatorics.
- Tokenization: Breaking language into tokens involves string manipulation and finite state machines.
- Graph Theory: Transformers and attention mechanisms are sometimes viewed as operating on graph-like structures.
- Logic and Formal Languages: Useful in designing rule-based prompts, symbolic AI, or interpretable AI systems.
Key Concepts to Know:
- Sets and functions
- Logic and boolean algebra
- Graphs and trees
- Combinatorics
5. Numerical Methods – Making It All Work in Practice
Handling the sheer scale of LLMs — often billions of parameters — requires efficient computation.
- Floating Point Precision: Tiny changes can lead to big errors; numerical stability is critical.
- Approximation Techniques: Methods like quantization or pruning are used to shrink models for deployment.
- Matrix Factorization: Used in model compression and embedding generation.
Key Concepts to Know:
- Floating point arithmetic
- Iterative methods
- Error analysis
- Vectorization and efficiency
Bonus: Math Isn’t Everything, But It’s the Foundation
You don’t need to be a math PhD to use LLMs or contribute to Gen AI projects. But having a solid understanding of the underlying math can help you:
- Debug models more effectively
- Design better architectures and prompts
- Optimize performance and interpret results
- Contribute to cutting-edge research
How to Get Started?
Here’s a roadmap to level up your math for Gen AI:
- Linear Algebra – Start with 3Blue1Brown’s Essence of Linear Algebra series.
- Probability & Statistics – Khan Academy or “Think Stats” by Allen B. Downey.
- Calculus – Focus on multivariable calculus and optimization.
- Practice – Use frameworks like PyTorch or TensorFlow to build toy models and understand how the math comes to life.
Final Thoughts
Math is the invisible engine that drives Gen AI. Whether it’s representing words as vectors or calculating gradients to improve predictions, mathematical thinking is embedded at every layer. The better we understand the math, the more we can unlock the full potential of LLMs — not just as users, but as creators and innovators.


